Sum of Interior Angles of a Polygon
A surface generated by rotating a line. What is the sum of the sizes of the interior angles of a polygon with 53 sides.

Polygon Worksheets Sum Of Interior Angles Of Polygons Worksheet Angles Worksheet Regular Polygon Worksheets
Interior Angle of a Regular Polygon Moderate Hone your skills in finding the measure of each individual interior angle with this set of printable worksheets featuring regular polygons with 20 sides.

. The sum of its exterior angles is N. The value of an interior angle of a regular polygon can be calculated if the number of sides of the regular polygon is known by using the following. Make sure each triangle here adds up to 180 and check that the pentagons interior angles.
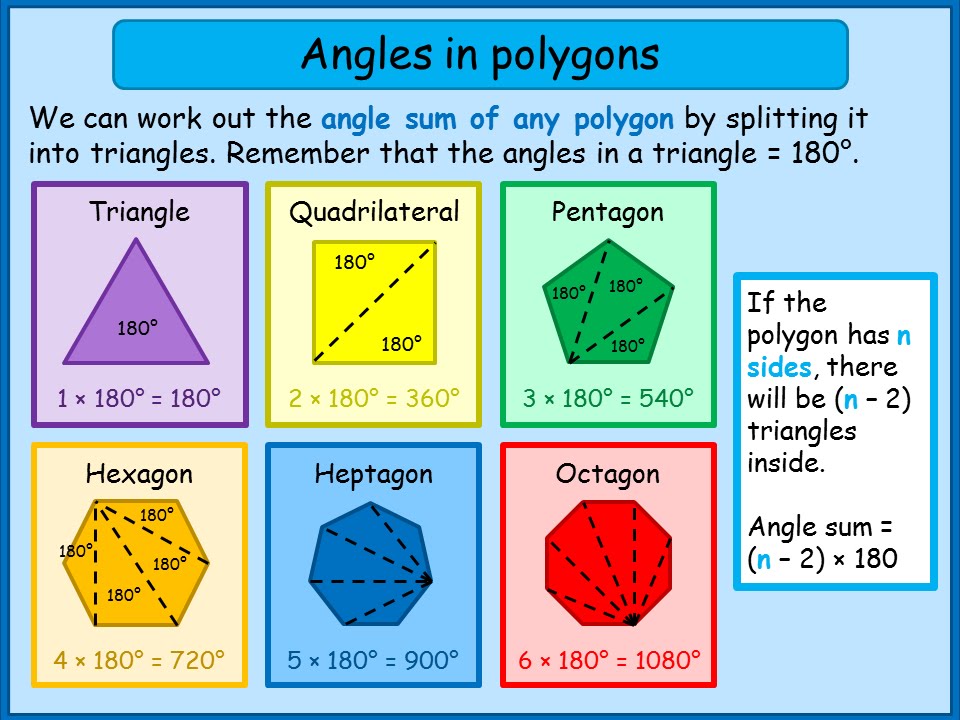
Sum of the interior angles of a polygon. It is always possible to. Sum of all interior angles n 2 180.
Euclidean geometry is assumed throughout. Angles in a straight line are a problem solving tool for many geometric problems. For any closed structure formed by sides and vertex the sum of the exterior angles is always equal to the sum of linear pairs and sum of interior angles.
Sum of the exterior angles of polygons 360 The sum will always. Angles in a triangle worksheets contain a multitude of pdfs to find the interior and exterior angles with measures offered as whole numbers and algebraic expressions. An Interior Angle is an angle inside a shape.
Interior Angles of a Polygon. Sum of the interior angles of a polygon with n sides n 2 180 For example. Interior angle The sum of the interior angles of a simple n-gon is n 2 π radians or n 2 180 degreesThis is because any simple n-gon having n sides can be considered to be made up of n 2.
A pentagon has 5 sides and can be made from three triangles so you know what. The formula is where is the sum of the interior angles of the polygon and equals the number of sides in the polygon. Hence we got the sum of exterior angles of n vertex equal to 360 degrees.
Area and perimeter in the coordinate plane I 6. The interior angles are formed between the adjacent sides inside the polygon and are equal to each other in the case of a regular polygon. Hence we can say now if a convex polygon has n sides then the sum of its interior angle is given by the following formula.
Since the angles in an equilateral triangle are equal we have to divide 180 by 3 to get the measure of an angle. Each corner has several angles. 16201114727 Each internal angle in an 11-sided.
The angle sum of this polygon for interior angles can be determined on multiplying the number of triangles by 180. All interior angles less than 180and all vertices point outwards away from the interior. It helps us in finding the total sum of all the angles of a polygon whether it is a regular polygon or an irregular polygon.
Step by step guide. Here a b c d e f 6 2 180 720 n 6 as given polygon has 6 sides 2. The interior angles of a shape are the angles.
The sum of the interior angles of a polygon of n sides can be calculated with the formula 180n-2. This property of a triangles interior angles is simply a specific example of the general rule for any polygons interior angles. Area between two shapes 10.
Learn to apply the angle sum property and the exterior angle theorem solve for x to determine the indicated interior and exterior angles. By using this formula we can verify the angle sum property as. The opposite of a regular polygon.
How many sides does a regular polygon have if each of its interior angles is 165. The number of interior angles is equal to the number of sides. A polygon with all sides and interior angles the same.
Divide the given sum of the interior angles by the number of angles in the polygon to find the size of each interior angle. Corresponding in character or kind. Jack is taller than Sarah but shorter than both Malika and Tania.
Set up the formula for finding the sum of the interior angles. The two most important ones are. We can find the measure of the interior angles of these triangles by remembering that all triangles have an angle sum of 180.
Area and perimeter in the coordinate plane II 7. Some lines containing interior points of a concave polygon intersect its boundary at more than two points. As with any simple polygon the sum of the internal angles of a concave polygon is π n 2 radians equivalently 180n 2 degrees where n is the number of sides.
Area and perimeter of similar figures 11. 1803 60 Each of the interior angles of an equilateral triangle is equal to. Who is the shortest.
The other part of the formula is a way to determine how many triangles the polygon can be divided into. Natasha is shorter than Sarah. Area of compound figures 9.
Of equal importance rank or degree. If your shape is regular just divide the sum of the interior angles by the number of sidesangles. Any polygon has as many corners as it has sides.
Area and circumference of circles 8. Sum of the exterior angles of polygons. The sum of interior angles of an 11-sided polygon is equal to 1620.
Lying in the same plane. Its interior angles add up to 3 180 540 And when it is regular all angles the same then each angle is 540 5 108 Exercise. Ratio of the adjacent side to the hypotenuse of a right-angled triangle.
Therefore if you have a regular polygon in other words where all the sides are the same length and all the angles are the same each of the exterior angles will have size 360 the number of sides. The value 180 comes from how many degrees are in a triangle. Two angles whose sum is a right angle.
Interior angles of polygons 3. Consider the following polygon with 6 sides. Regular polygons are always convex.
What is the Sum of the Interior Angles of a Polygon. No matter how you position the three sides of the triangle the total degrees of all interior angles the three angles inside the triangle is always 180. What is the height one of the legs and the hypotenuse of an isosceles right triangle that has an area of 800 square.
Ex 32 Class 8 Maths Question 4. So for example each of the exterior angles of a hexagon are 3606 60. Each interior angle n sum of interior angles n 1 8 0 n 2 If your shape is irregular and you have the values of all the other interior angles you can find the missing angle by subtracting your given angles from the sum.
Determine the measure of the interior angles of a regular 11-sided polygon. These printable exercises are customized for students of 6th grade through. None of these three statements holds for a convex polygon.
Since the polygon is regular we can use the sum obtained in the previous example and divide by 11 since all the angles are equal. Therefore N 180n 180n-2 N 180n 180n 360. Malika is shorter than tania.
After examining we can see that the number of triangles is two less than the number of sides always. Sum of all exterior angles of a regular polygon 360 Number of sides Hence the number of sides 15. Area of triangles and quadrilaterals 5.
Angles in a triangle. If we split any straight line into smaller angles all of these angles would add to make 180 the same as with a triangle. A shape with a circular base and sides tapering to a point.
Each side may a different length each angle may be a different measure. Let re be the number of sides of a regular polygon. We can therefore state that the sum of angles on a straight line is equal to 180.

Interior Angles Of Polygons Quadrilaterals Interior And Exterior Angles Polygon

Http Www Aplustopper Com Interior Angle Regular Polygon Interior Angles Of Regular Polygons Regular Polygon Studying Math Exterior Angles
11 Angle Sum Of Any Polygon Maths Tutorials Youtube Math Tutorials Math For Kids Math Activities

Image Result For Polygon Interior Angles Regular Polygon Math Charts Polygon
0 Response to "Sum of Interior Angles of a Polygon"
Post a Comment